Problem sofy, który od dziesięcioleci prześladował matematyków i bohaterów serialu "Przyjaciele", został w końcu rozwiązany

Problem matematyczny, który jest dwuwymiarowym modelem rzeczywistego problemu przesuwania sofy w mieszkaniu lub domu, został w końcu rozwiązany. Po raz pierwszy pojawił się on w 1966 roku i był źródłem zagadek dla matematyków i bohaterów serialu Przyjaciele.

Problem ten definiuje największą sofę, która może zmieścić się w rogu o danej szerokości, z czym bohaterowie serialu zmierzyli się w odcinku wyemitowanym w 1999 roku. Matematyk z Korei Południowej znalazł rozwiązanie tego problemu i opublikował swoje wyniki na serwerze preprintów ArXiv, donosi Live Science.

Problem został sformułowany przez austriacko-kanadyjskiego matematyka Leo Mosera. Zapytał on o największą możliwą powierzchnię pojedynczego kształtu w jednej płaszczyźnie, który mógłby poruszać się wokół prostokątnego rogu korytarza o jednostkowej szerokości. Na pierwszy rzut oka może się to wydawać łatwe, ale w rzeczywistości nie jest, ponieważ zadanie wymaga zarówno obliczenia maksymalnej powierzchni, jak i przesunięcia kształtu.

A teraz, 2 grudnia, Jineon Baek, doktorant matematyki na Uniwersytecie Yonsei w Korei Południowej, znalazł rozwiązanie, które opublikował na nieco ponad 100 stronach dowodów matematycznych. Baek odkrył, że dla korytarza o szerokości 1 jednostki maksymalna powierzchnia wyimaginowanej sofy może wynosić 2,2195 jednostki - zawężając odpowiedź do znanego wcześniej zakresu od 2,2195 do 2,37 jednostki. Dowód nie został jeszcze opublikowany w recenzowanym czasopiśmie i będzie musiał zostać opracowany przez innych matematyków, aby ustalić, czy rzeczywiście jest optymalny.

W 1992 roku matematyk Joseph Gerwer z Rutgers University ustalił dolną granicę powierzchni sofy na 2,2195 jednostki. Jednak lata debat nad tym, czy sofa może mieć większą powierzchnię, doprowadziły międzynarodową grupę matematyków w 2018 roku do zasugerowania, że górna granica maksymalnej powierzchni sofy wynosi 2,37 jednostki.

Oznacza to, że Ross mógłby uniknąć problemu, gdyby wziął pod uwagę tylko sofę Gerver z 18 zakrzywionymi sekcjami i maksymalną powierzchnią 2,2195 jednostki.

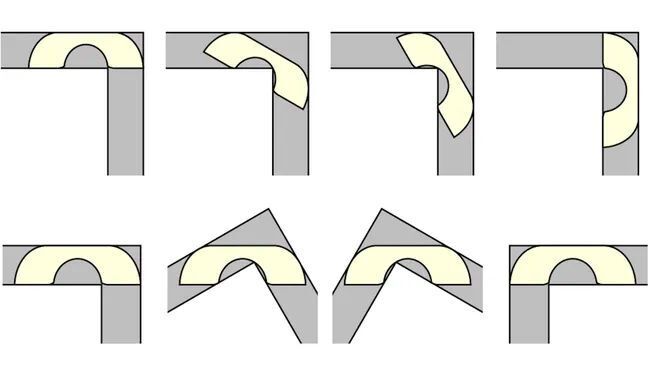
Sofa Gerver to szeroka sofa w kształcie litery U z zakrzywionym "siedziskiem", które może przecisnąć się za róg bez zwisania. Pytanie brzmiało, czy ta starannie zaprojektowana sofa, wykonana z 18 pojedynczych krzywizn, była naprawdę największym i najbardziej optymalnym kształtem, który można zmienić. Beck opracował geometrię kształtu i jego ruchu i stwierdził, że rozwiązanie Gerwera było w rzeczywistości poprawne.

Tylko zweryfikowane informacje są dostępne na naszym kanale Telegram OBOZ.UA i Viber. Nie daj się nabrać na podróbki!